Walk, Path and Circuit in Graphs
Walk:
A walk is a way of getting from one vertex to another, and consists of a sequence of edges, one following the other.
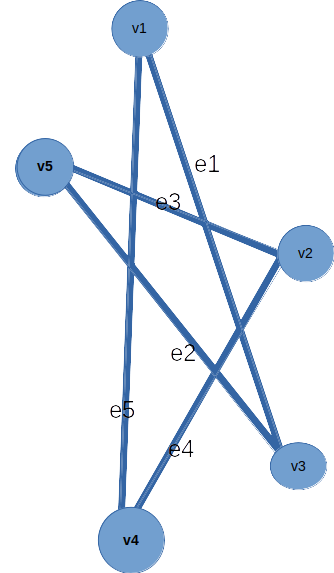
For example, in graph G, v1– v3– v5 (also v1e1 v3e2 v5) is a walk of length 2, and v1-v4-v2-v5-v3-v1-v4 is a walk of length 6.
-
The length of a walk is the number of edges in the walk.
-
A walk of length zero is a trivial walk.
Path:
A path is a walk with no repeated vertices.
In graph G, v1– v3– v5 is a path but v1-v4-v2-v5-v3-v1 is not a path as vertex v1 repeats.

Trial:
A trail is a walk with no repeated edges.
In graph G, v1– v3– v5 is a trial but v1-v4-v2-v5-v3-v1-v4 is not a trial because the edge v1-v4 is repeated.

Circuit:
A circuit is a closed trail
In graph G, v1-v4-v2-v5-v3-v1 is a closed trail and so it is a circuit.
A trivial circuit has a single vertex and no edges.
Ex. v1 is a trivial circuit.
A circuit may also be called as cycle, elementary cycle, circular path and polygon.

Length of a walk:
Length of a walk is nothing but the number of edges in that walk.
In graph G, length of the walk v1-v4-v2-v5-v3-v1 is 5.
‘v1‘ is a walk of length 0.

Distance:
Distance between two vertices is the length of the shortest path between them.
In graph G, distance between v1 and v2 is 2. Because the shortest path among the two paths v1– v4– v2 and v1– v3– v5– v2 between v1 and v2 is of length 2.

Eulerian Graph:
A walk is Eulerian if it includes every edge of the graph only once and ending at the initial vertex.
A graph that contains an Eulerian walk is said to be an Eulerian Graph.
Eulerian walk: v1-v3-v5-v2-v4-v1 (in graph G)
As graph G contains an Eulerian walk it is an Eulerian Graph.

Hamiltonian Graph:
A walk is Hamiltonian if it includes every vertex of the graph only once and ending at the initial vertex.
A graph that contains a Hamiltonian walk is said to be a Hamiltonian Graph.
v1-v3-v5-v2-v4-v1 (in graph G)
As graph G contains a Hamiltonian walk it is a Hamiltonian Graph.

Vertex cut set:
A set of vertices in a graph G is said to be a vertex cut set if its removal makes G, a disconnected graph. In other words, the set of vertices whose elimination will increase the number of components of G.
For example, in our graph G the set {v4, v5} is a vertex cut set because if we remove these two vertices G will become disconnected (Graph ii).


Cut Vertex:
A single vertex in a graph G is said to be a cut vertex if its removal makes G, a disconnected graph. In other words, a cut vertex is the single vertex whose elimination will increase the number of components of G.
For example, in our graph vertex v2 is a cut vertex because if we remove v2, our graph will become disconnected (graph ii). v4 is also a cut vertex.


Connectivity:
The minimum number of vertices whose removal disconnects a graph is said to be the connectivity of the graph.
For example, in our graph vertex v2 is a cut vertex because if we remove v2, our graph will become disconnected (graph ii). So the connectivity of Graph i is 1.


Block:
Block is a connected graph with no cut vertex.
The graph given is a block because elimination of any single vertex will not make our graph disconnected.

Edge cut set:
A set of edges in a graph G is said to be an edge cut set if its removal makes G, a disconnected graph. In other words, the set of edges whose elimination will increase the number of components of G.
For example, in our graph G the set {e1, e2} is an edge cut set because if we remove these two edges G will become disconnected (Graph ii).


Bridge:
An edge in a graph G is said to be a bridge if its removal makes G, a disconnected graph. In other words, bridge is the single edge whose elimination will increase the number of components of G.
For example, in our graph edge e6 is a bridge because if we remove e6, our graph will become disconnected (graph ii). e7 is also a bridge.


Bipartite Graph:
A graph is said to be Bipartite if its vertex set V can be split into two sets V1 and V2 such that each edge of the graph joins a vertex in V1 and a vertex in V2.
G is a bipartite graph because all edges have one vertex in each set V1 and V2.

Complete Bipartite Graph:
A bipartite graph is said to be complete if there exist an edge between every pair of vertices from V1 and V2.
G is a complete bipartite graph because there exist an edge between every pair of vertices from V1 and V2, viz., {(v1,v3), (v1,v4), (v1,v5), (v2,v3), (v2,v4), (v2,v5)}.
