Relations: Definitions and Types

Cartesian Product:

Cartesian Product of two sets A and B, written as A X B, is the set of all pairs with first element from set A and second element from set B, written with in ‘(‘ and ‘)’, separated by comma ‘,’.  These pairs are also called ordered pairs as they follow an order in placement.  Therefore, A X B is not the same as B X A (in which the first element is from B and the second element is from A).

If A={a, b} and B={1, 2} then

AXB={(a, 1),(a,2), (b, 1), (b, 2)}  and
BXA ={(1, a), (1, b), (2, a), (2, b)}

If C={x} then

AXBXC={(a, 1),(a,2), (b, 1), (b, 2)}  XC
Therefore, AXBXC={(a, 1,x),(a,2,x), (b, 1,x), (b, 2,x)}  XC and

     BXAXC={(1, a,x),(1, b,x), (2, a,x), (2, b,x)}

That is, AXBXC is the set of all ordered triplets in which the elements occupy their respective places as in the name.  That is, elements of the first set take first place in the triplet, elements of the second set take second place and elements of third set take third place in the triplet.
In a similar manner, we may find the cartesian product of any number of sets.

Cardinality of AXB:

If |A| = m and |B| = n then we could write mn pairs between A and B.  Therefore, Cardinality of AXB,

|AXB| = mn

In our example,

|A| = 2 and |B| = 2 and so,
|AXB| = 4.
|C| = 1 and so |AXBXC| = |AXB| * |C|= 4*1 = 4.

Relations on Sets:

A relation R between two sets A and B is a subset of their cartesian product AXB.  In other words, for every subset of AXB there corresponds a relation R between A and B.  Therefore, there exist

2mn, (number of subsets of AXB)

relations between A and B.

Example:

If A={a, b} and B={1, 2} then

AXB={(a, 1),(a,2), (b, 1), (b, 2)}  and

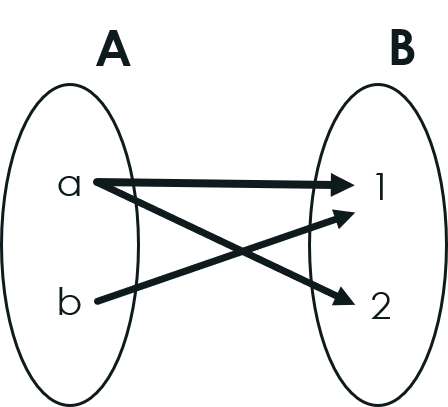
For, R={(a, 1),(a,2), (b, 1)} where R⊆ AXB,

  1. a related to 1 (written as aR1)
  2. a related to 2 (written as aR2) and
  3. b related to 1 (written as bR1) is a relation between A and B.

For R0=∅, ∅⊆AXB, we say that no elements of A and B are related.

Pictorial representation of Relation R:

sample

Pictorial representation of Relation R2: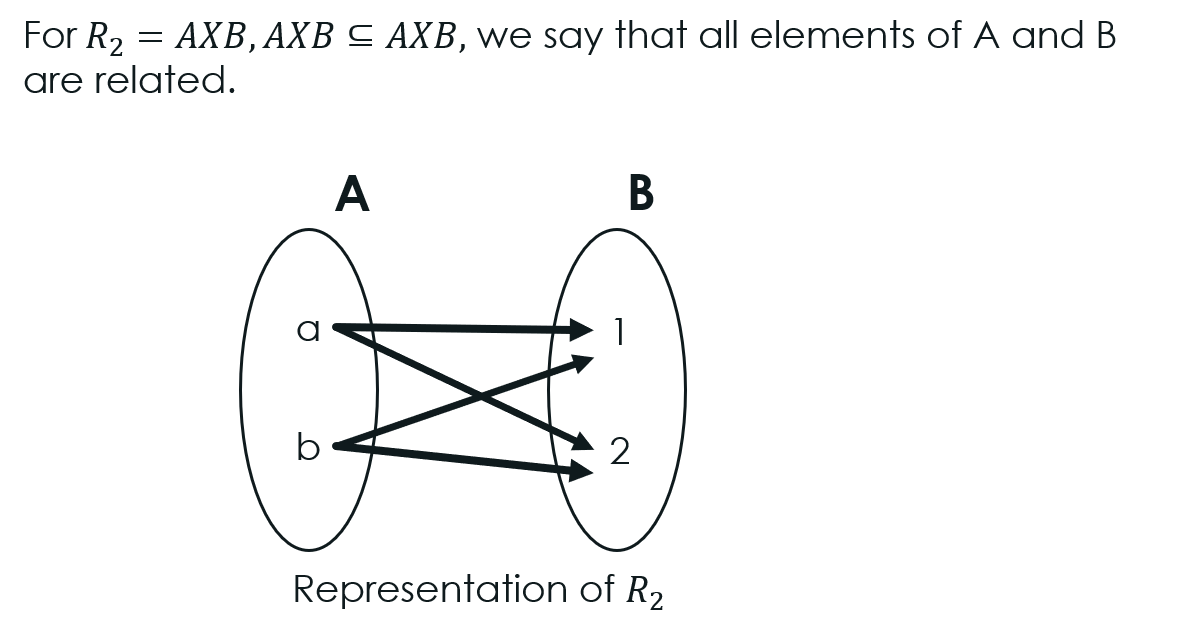sample

Domain of Relation R:

For a relation R subset of AXB, the subset of A which contains those elements of A which are related to some element (or elements) of B is said to be the domain of R.  Symbolically,

Domain of R = {a∈A|aRb for some b∈B}

Range of Relation R:

For a relation R subset of AXB, the subset of B which contains those elements of B which are related to some element (or elements) of A is said to be the range of R.  Symbolically,

Range of R = {x∈B|aRx for some a∈A}

Example:

For R1={(a,1)}⊆AXB, the domain of R1  is the singleton set {a}⊆A because b is not related to any element of B.
The range of R1  is the singleton set {1}⊆B because 2 is not related to any element of A.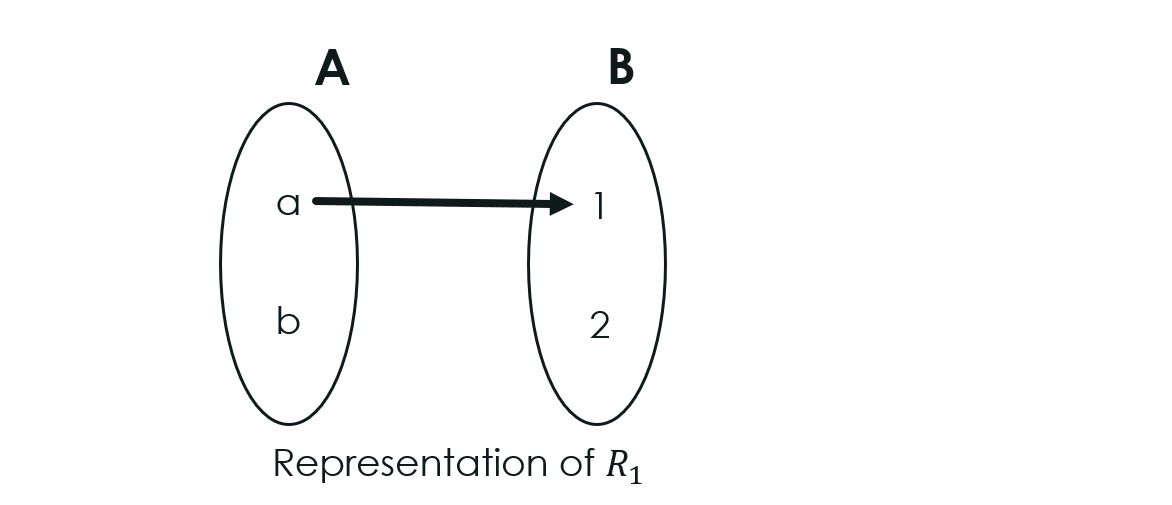
sam

Complement of Relation R:

The relation corresponds to the complement of the subset R of AXB is said to be the complement relation of R.

If A={a, b} and B={1, 2} then

AXB={(a, 1),(a,2), (b, 1), (b, 2)}.
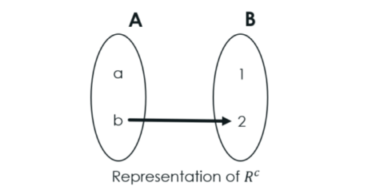
For, R={(a, 1),(a,2), (b, 1)} where R⊆ AXB,
Rc={(b, 2)}

is the complement relation of R.
In Rc,  only b is related to 2 (bR2).

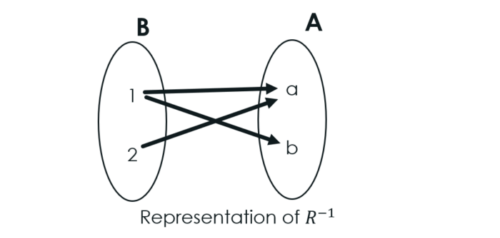
Inverse of Relation R:

The relation having the range of R as its domain and the domain of R as its range is said to be the inverse relation of R.  In other words, if R is a subset of AXB then inverse of R is a subset of BXA.
If A={a, b} and B={1, 2} then

AXB={(a, 1),(a,2), (b, 1)}.

For, R={(a, 1),(a,2), (b, 1)} ⊆ AXB, A is the domain of R and B is the range of R.Then
R-1={(1, a),(2,a), (1, b)}⊆ BXA, is the inverse relation of R. For R-1, B is the domain and A is the range.

Types of Relations:

Consider the Cartesian product AXB , where A and B are two non-empty sets.  Now we take the relations on A to B which are subsets of AXB and classify them.  
For R0=∅, ∅⊆AXB, we say that no elements of A and B are related. This relation R0 is said to be the void relation or empty relation.  
For R2=AXB, AXB⊆AXB, we say that all elements of A and B are related. This relation R2 is said to be the universal relation on A.
Any relation R⊆AXA, is said to be reflexive iff for any a∈A, aRa.  Equivalently, (a, a) ∈ R for every a∈A. Suppose A = {a, b} then

R = {(a, a), (a, b), (b, b)}

is a reflexive relation on A. But

Rx={(a, b), (b, b)}

is not reflexive since for a∈A the element (a, a)∉ Rx.
Any relation R⊆AXA, is said to be symmetric iff for every aRb there must be bRa. Equivalently, (a, b)∈R⇔(b, a)∈R.
Suppose A = {a, b} then

R = {(a, b), (b, a)}

is a symmetric relation on A.
But

Rx = {(a, b), (b, b)}

is not symmetric since for the element (a, b)∈Rx the element (b, a)∉Rx.

Any relation R⊆AXA, is said to be anti-symmetric if aRb and bRa implies a=b.

Consider the set of natural numbers N = {1, 2, 3, 4, 5, …}

The relation ‘≤’  is an anti-symmetric relation on N.

For, if x ≤ y & y ≤ x then x = y.

More clearly, x is less than or equal to y and y is less than or equal to x then it is not possible for any natural number that x < y & y < x and hence implies that x = y.

Therefore, ‘≤’ is an anti-symmetric relation on N.

Any relation R⊆AXA, is said to be transitive if aRb and bRc then there must be aRc.

Equivalently, (a, b) ∈ R and (b, c) ∈ R then (a, c)∈ R.

Suppose A = {a, b, c} then

R = {(a, b), (b, c), (a, c)}

is a transitive relation on A.

But

Rx={(a, b), (b, c), (a, c), (c, a)}

is not transitive since for the pair (b, c)∈ Rx and (c, a)∈ Rx the element (b, a) ∉Rx. Also, for the pair (a, c)∈ Rx and (c, a)∈ Rx the element (a, a) ∉ Rx.

Any relation R⊆AXA, is said to be an equivalence relation on A if R is reflexive, symmetric and transitive.

Equivalently,

  1. (a, a) ∈ R, for every a∈A (reflexive)
  2. (a, b) ∈ R   ⇔     (b, a) ∈ R (symmetric)
  3. (a, b)∈R and (b, c) ∈ R then (a, c) ∈ R (transitive)

Suppose A = {a, b} then

R = {(a, b), (a, a), (b, b), (b, a)}

is an equivalence relation on A since

  1. (a, a) ∈ R and (b, b) ∈R so R is reflexive
  2. (a, b) ∈ R  implies (b, a) ∈ R & (b, a) ∈ R  implies (a, b) ∈ R so R is symmetric
  3. (a, b) ∈ R and (b, a) ∈ R then (a, a)∈ R,

    (a, b) ∈ R and (b, b) ∈ R then (a, b) ∈ R,

    (a, a) ∈ R and (a, b) ∈ R then (a, b) ∈ R,

    (b, a) ∈ R and (a, b) ∈ R then (b, b) ∈ R,

    (b, a) ∈ R and (a, a) ∈ R then (b, a) ∈ R,

    (b, b)∈ R and (b, a) ∈R then (b, a) ∈ R so R is transitive.

Therefore, R is an equivalence relation.

But

Rx={(a, b),(a, a)}

is not an equivalence relation since

(b, b) ∉ Rx hence Rx is not reflexive.

The relation which does not satisfy any one of the three conditions is not an equivalence relation where as the relation which satisfy all the three is an equivalence relation.

POSET (Partially Ordered Set):

Any relation R⊆AXA, is said to be a Partial Ordering on A if R is reflexive, anti-symmetric and transitive.

Equivalently,

  1. aRa, for every a∈A (reflexive)
  2. aRb and bRa   ⇔     a = b (anti-symmetric)
  3. aRb and bRc then aRc (transitive)

Then the set A together with this partial ordering R is said to be a POSET and is written as (A, R).

Example:

Consider the set of natural numbers N = {1, 2, 3, 4, 5, …} and the relation ‘≤’.

Clearly, the relation ‘≤’  is

  1. n≤n for any n∈ N (reflexivity)
  2. m≤n and n≤m  ⇔     m = n (anti-symmetry)
  3. l≤m and m≤n then l≤n (transitivity)

Therefore, ‘≤’ is a partial ordering on N and hence (N, ‘≤’ ) is a POSET.

Maximal Element:

The element ‘a’ of N is said to be the maximal element of N if n≤a, for every n∈ N.

Minimal Element:

The element ‘a’ of N is said to be the minimal element of N if a≤n, for every n∈ N.

Bounded set:

If there exist a maximal and a minimal element for a set then that set is said to be a bounded set.

Linearly Ordered Set or Totally ordered set:

Any relation denoted by ‘≤’, is said to be a Linear Ordering (or Total Ordering) on A if ‘≤’ is reflexive, anti-symmetric, transitive and comparable.

Equivalently,

  1. a≤a, for every a∈A (reflexivity)
  2. a≤b and b≤a  implies a = b (anti-symmetry)
  3. a≤b and b≤c then a≤c (transitivity)
  4. either a≤b or b≤a for any a, b∈A (comparability or trichotomy)

Then the set A together with this linear ordering (or total ordering) ‘≤’ is said to be a Linearly Ordered Set or Totally Ordered Set and is written as (A, ‘≤’).

Example:

Consider the set of integers N = {1, 2, 3, 4, 5, …} and the relation ‘≤’.

Clearly, the relation ‘≤’  is

  1. n≤n for any n∈ N (reflexivity)
  2. m≤n and n≤m  ⇔     m = n (anti-symmetry)
  3. l≤m and m≤n then l≤n (transitivity)
  4. m≤n for any m,n∈ N

Therefore, ‘≤’ is a linear ordering (or total ordering) on N and hence (N, ‘≤’ ) is a linearly ordered set (or totally ordered set).

Previous
Next