Operations on Sets
Venn Diagram:
Venn diagram is the pictorial representation of sets and their operations which was named after John Venn who popularized this representation and usage. Generally, the universal set will be represented by a rectangle and other subsets of this universal set will be represented by circles or ellipses.
Union of two Sets:
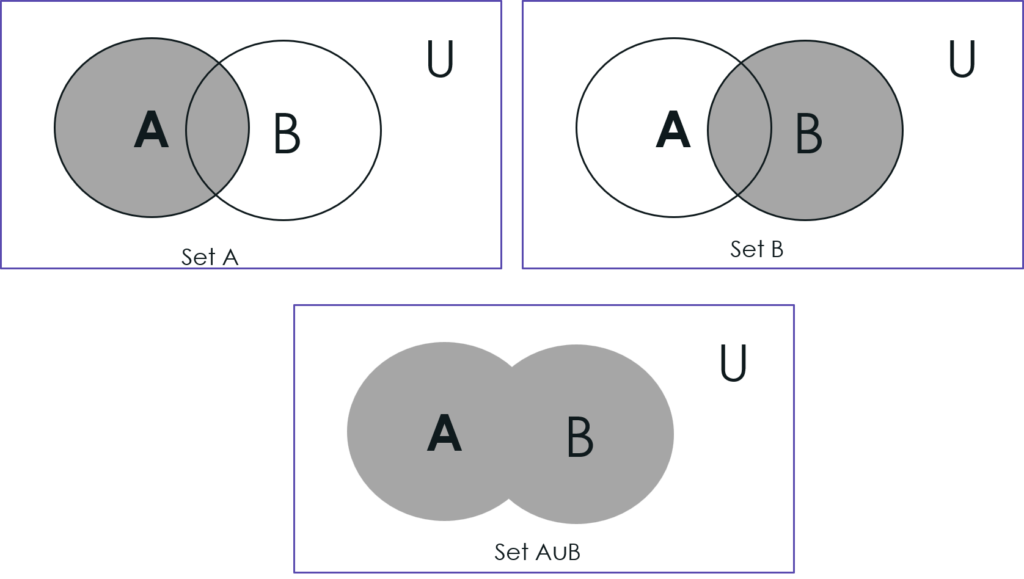
The set of all elements of both sets is said to be the union of the two sets. In other words, the elements of the union of A and B are either the elements of A or the elements of B.
Examples:
If A = {a, b, c, d} and B = {1, 2, 3, 4, 5, 6} then their union will be,A ∪ B = {a, b, c, d, 1, 2, 3, 4, 5, 6} and
Cardinality of A ∪ B = Cardinality of A + Cardinality of B
i.e., |A∪B| = |A| + |B|
= 4 + 6 = 10
Venn Diagram of Union of Sets:
Intersection of two SET:
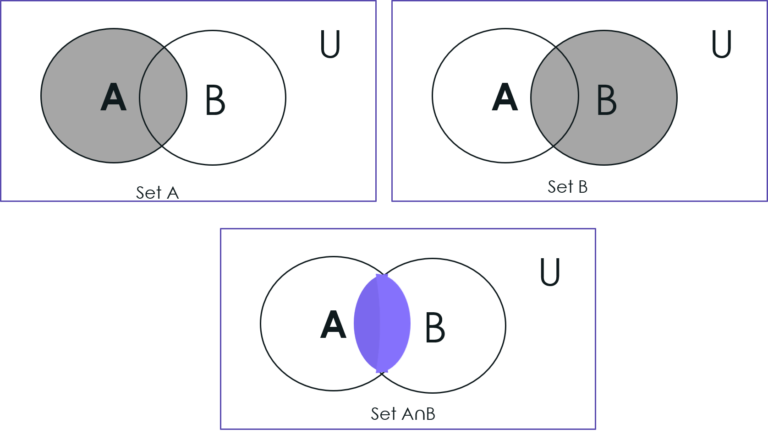
The set of all elements which are elements of both sets is said to be the intersection of two sets. In other words, the elements of the intersection of A and B are elements of both A and B.Examples:
If A = {a, b, c, d} and B = {c, d, e, f} then their intersection will be,A ∩ B = {c, d} and Cardinality of A ∩ B = |A ∩B | = 2
Venn Diagram of Intersection of Sets:
Complement of a Set:
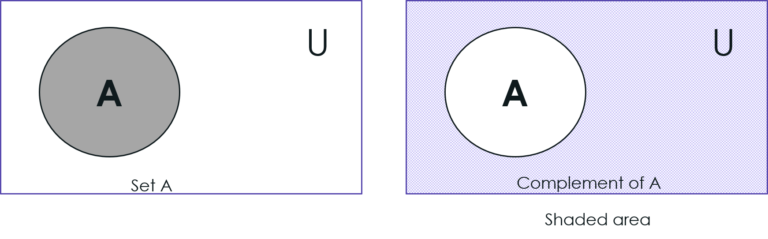
The set of elements of the Universal set which are not the elements of a set A is said to be the Complement of A.
𝑖.𝑒., 𝐴𝑐=𝑈−𝐴
U = {a, b, c, …, z} and A = {a, b, c, d} thenComplement of A = AC = {e, f, g, h, i, …, z}
Venn Diagram of a Set:
Difference of two Sets:
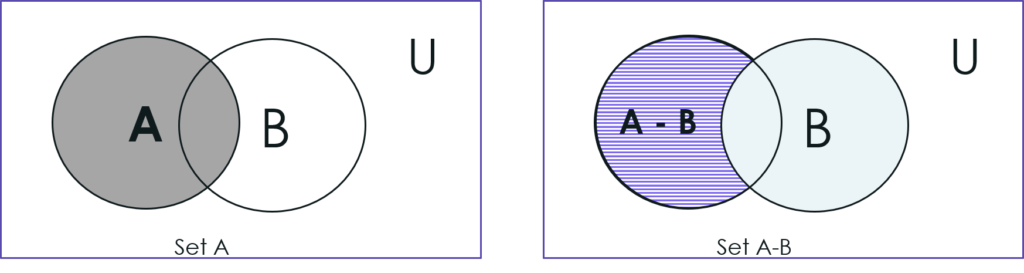
The difference of two sets A and B, denoted by A-B, is the set of all elements of A which are not elements of B. In other words, A-B is the complement of B relative to A.
Examples:
If A = {a, b, c, d} and B = {c, d, e, f} then their difference will be obtained by eliminating the elements of B from A. That is,
A – B={a, b}
Venn Diagram of difference of Sets:
Equalities of Sets:
- X∪X=X
- X∩X=X
- X∪Y=Y∪X
- X∩Y=Y∩X
- (X∪Y)∪Z=X∪(Y∪Z)
- (X∩Y)∩Z=X∩(Y∩Z)
- 𝑋∪(𝑌∩𝑍)=(𝑋∪𝑌)∩(𝑋∪𝑍)
- 𝑋∩(𝑌∪𝑍)=(𝑋∩𝑌)∪(𝑋∩𝑍)
- 𝑋∪∅=𝑋
- 𝑋∩∅=𝑋
- 𝑋∪𝑈=𝑈
- 𝑋∩𝑈=𝑋
- 𝑋∪𝑋𝑐=𝑈
- 𝑋∩𝑋𝑐=∅
- (𝑋𝑐)𝑐=X
- 𝑋−𝑌=𝑋∩𝑌𝑐
- (𝑋∪𝑌)𝑐=𝑋𝑐∩𝑌𝑐
- (𝑋∩𝑌)𝑐=𝑋𝑐∪𝑌𝑐
- 𝑋⊆𝑌 𝑖𝑓𝑓 𝑋∪𝑌=Y
- 𝑋⊆𝑌 𝑖𝑓𝑓 𝑋∩𝑌=X