Graph Theory: A Beginner's Guide

Graph theory, a branch of mathematics concerned with networks of points connected by lines. The subject of graph theory had its beginnings in recreational maths problems, but it has grown into a significant area of mathematical research.

In recent years, graph theory has established itself as an important mathematical tool in a wide variety of subjects, ranging from operational research and chemistry to genetics and linguistics, and from electrical engineering and geography to sociology and architecture. At the same time it has also emerged as a worthwhile mathematical discipline in its own right.

Graph theoretical techniques are highly used by computer science applications especially in modelling and routing in networks.  Lets start…

Table of Contents:

  1. Edges, Vertices & Graphs
  2. Null Graphs & Complete Graphs
  3. Finite & Infinite Graph
  4.  Loops & Parallel Edges
  5. Simple Graph
  6. Adjacent Vertices & Adjacency Matrix
  7. Incidence & Incidence Matrix
  8. Isolated & Pendent Vertices
  9. Regular Graph & Edge Series
  10. Isomorphism of Graphs
  11. Operations on Graphs
  12. Connected Graphs
  13. Disconnected Graphs
  14. Components of a Disconnected Graph

Edges:

The lines are called edges

Vertices:

The points (i.e. the point of intersection of lines) are called vertices

graph theory

Graph:

A graph is nothing but a combination of edges and their intersection points. Based on their intersection types the graphs are named differently. For example, a simple graph, a tree, a connected graph etc.

Formally,

A pair G = (V , E ) consists of a non-empty set V of vertices and a set E of edges is said to be a graph. 

graph theory

Null Graph:

A graph G = (V , E ) with a non-empty vertex set (V) and an empty edge set (E) is said to be a null-graph.  In Other words, graph with no edge between any pair of vertices is a null graph.

G0 is a null graph.

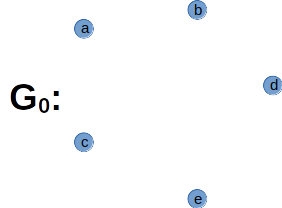
V = {a, b, c, d, e}

E = ∅

G0 = (V, E)

 

 

Complete Graph:

A graph with an edge between any pair of vertices is said to be a complete graph.

K4 is a complete graph with 4 vertices because there exists an edge between every pair of vertices. 

complete graph

V = {a, b, c, d}

E =  {e1, e2, e3, e4, e5, e6}

K4 = (V, E)

 

 

Other Names:

  • Graph: Linear complex, 1-complex, one-dimensional complex
  • Vertex: Node, Junction, Point, 0-cell, 0-simplex
  • Edge: Branch, Line, Element, 1-cell, Arc, 1-simplex

Finite Graph:

A graph G=(V, E) is said to be a finite graph if both V (the set of vertices) and E (the set of edges) are finite.

Infinite Graph:

A graph G=(V, E) is said to be a finite graph if both V (the set of vertices) and E (the set of edges) are finite.

Loop:

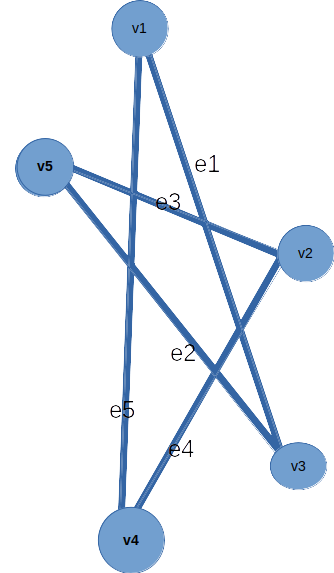
If an edge has only one endpoint(i.e. starts and ends at the same vertex) then it is said to be a loop.

In graph G, edge e6 is a loop because it starts and ends at the same vertex v2. 

A graph with loop is known to be a Pseudo-graph.

Since our graph G has a loop it is a Pseudo-graph

graph theory

Multiple or Parallel Edges:

If two or more edges connect same pair of vertices then these edges are said to be multiple or parallel edges between the respective pair of vertices.

In graph 1.2, edges e3 and e6 are parallel (or multiple) edges as they both starts and ends at the same pair of vertices (v2, v5).

A graph with multiple (or parallel) edges is known to be a multi-graph.

Since our graph G has parallel edges it is a multi-graph.

Graph 1.2

Simple Graph:

A graph is said to be simple if it has no loops or multiple edges.  In other words, a graph is simple if there is at most one edge between any given pair of vertices.

Edges in a simple graph may be given by a pair of its incident vertices {vi, vj} because there exist no other edges (parallel edges or loops) between these two vertices.

Graph G is a Simple Graph.

spanning subgraph

Pseudo Graph:

A graph is said to be a pseudo graph if it has loops or multiple edges or both.

Graph G is a Pseudo Graph.

graph theory

Adjacent Vertices:

If a pair of vertices have at least an edge connecting them then these vertices are said to be adjacent vertices.

For example in graph G, vertices v5 – v2, v5 – v3, v4 – v7 are all adjacent vertices because there is an edge between each pair.

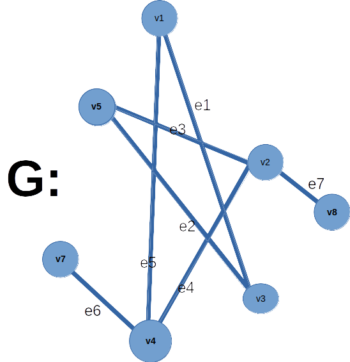
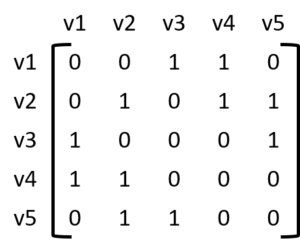
Adjacency Matrix:

Matrix which represents the adjacency of vertices is said to be the adjacency matrix.

In our example, v1 is adjacent to v3 and v4 so that places has entry 1.  There is an edge from v2 to v2 (loop) so it has entry 1.  There is no edge between v1 and v2 so that pair has entry 0.

graph theory

Neighborhood of a Vertex :

The set of all vertices adjacent to a vertex v is said to be the neighborhood of v.  It is denoted by N(v).

In our example, v1 is adjacent to v3 and v4 so that the neighborhood of v1, N(v1) = {v3, v4}.

Likewise, v2 is adjacent to v4, v5 and to itself.  Because there is an edge from v2 to v2 (loop).  So the beighborhood of v2, N(v2) = {v2, v4, v5}.

graph theory

Adjacent Edges:

Two non-parallel edges are said to be adjacent if they both intersect at a common vertex.

For example, in graph G, edges e3 and e7 are intersecting at vertex v2, so they are adjacent to each other.

Incidence:

A pair (v, e) of a vertex and an edge is said to be incident with or incident on or incident to each other, if vertex v is an end point of edge e (starts or ends at v).

For example, in graph G, edge e3 starts(or ends) at vertex v2, so they are said to be incident to each other.

Incidence Matrix:

Matrix which represents the incidence of a vertex-edge pair is said to be the incidence matrix.

For example, edge e1 is incident to vertices v1 and v3 and so the two places have entry 1.  Edge e6 is incident to v2 only; so e6 column has only one unity.

graph theory

Degree:

The number of edges incident at a vertex is said to be the degree of that vertex.

For example, in graph G, edges e2, e3 and e7 are incident at vertex v2, so the degree of v2 is 3 and written as, d(v2) = 3.

Isolated Vertex:

A vertex is said to be an isolated vertex if no edge is incident to it.   In other words, a vertex of degree ‘0’ is an isolated vertex.

In graph G0, every vertex is an isolated vertex because the degree of all vertices is 0.

Pendent or End Vertex:

A vertex is said to be a pendant vertex if, only one edge is incident to it.  In other words, a vertex of degree ‘1’ is a pendent vertex.

In graph G, v7 and v8 are pendant vertices as d(v7) =1 and d(v8)=1.

Regular Graph:

If the degree of all vertices in a graph are equal then that graph will be called as a regular graph.  If the degree is r then it may also be called as r-regular graph.

In graph G, every vertex is of degree 2 and so G is a regular graph.  It may be called as 2-regular graph.

spanning subgraph

Edge Series:

Two edges are said to be in series if they are adjacent and their common vertex has no other edge incident to it.  In other words, two adjacent edges are said to be in series if their common vertex is of degree 2.

In graph 1.3, d(v1)=2,  d(v5)=2 and d(v3)=2 and so edges e1-e3, e2-e3 and e1-e2 are said to be in series.

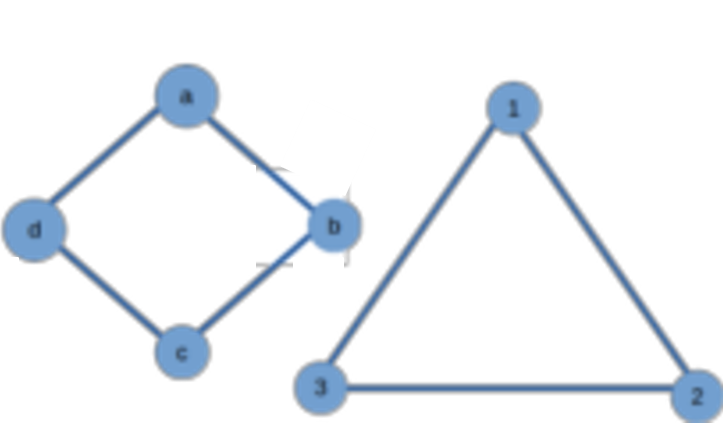
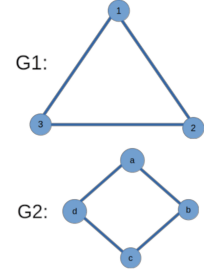
Isomorphism of Graphs:

Two graphs G1 and G2 are said to be Isomorphic if there is a one-one correspondence between the vertices of G1 and G2 such that, the number of edges joining any two vertices of G1 is equal to the number of edges joining the corresponding vertices of G2 .

In our graphs, the vertex ‘a’  in G1 corresponds to the vertex A in G2.  Likewise vertices b,c,d,e,f in G1 corresponds to vertices B,C,D,E,F in G2 respectively.

For vertex ‘a’ in G1, e and c are adjacent and there are 2 edges incident to it.  Likewise for vertex ‘A’ in G2, E and C are adjacent and it also has two edges incident to it.  

Likewise, all corresponding vertices in G1 and G2 have same number of edges incident to them.  And adjacent vertices in G1 are adjacent in G2 also.

Therefore, our graphs G1 and G2 are Isomorphic.

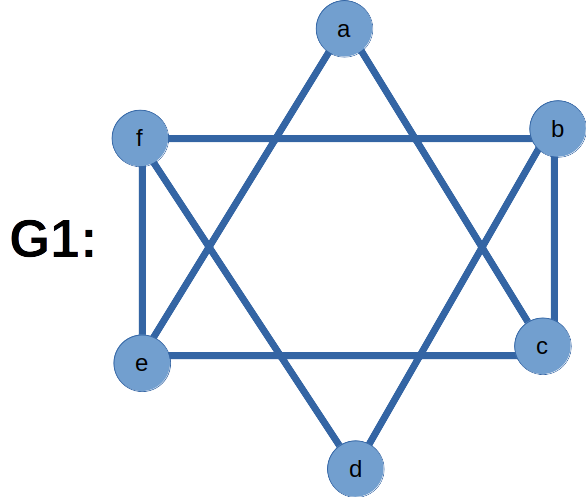
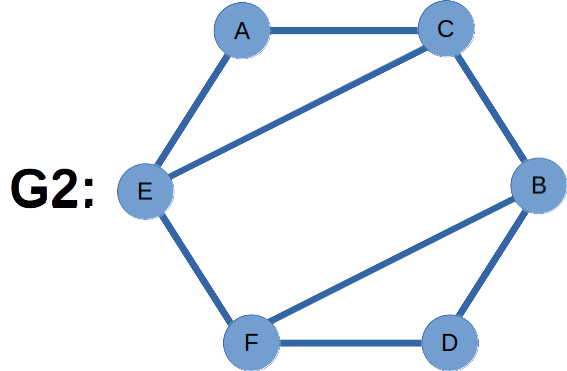
Operations on Graphs:

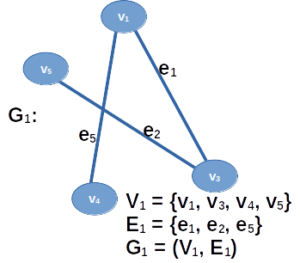
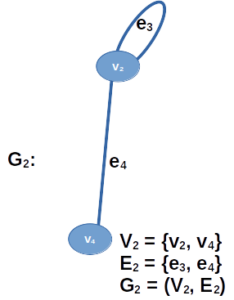
Union of Graphs:

If G1={V1,E1} and G2={V2,E2} are two graphs  then the union of G1 and G2 is the graph G1UG2={V1UV2, E1UE2}.

Intersection of Graphs:

If G1={V1,E1} and G2={V2,E2} are two graphs then the intersection of G1 and G2 is the graph G1∩G2={V1∩V2, E1∩E2}.

In our example, G1∩G2 is simply the single vertex v4.

  G= (V, E)

Connected Graph:

A graph is said to be connected if it cannot be expressed as the union of two graphs.  In other words, a graph is said to be Connected if there exist a walk between every pair of its vertices. 

In Graph 3.2(a), G is a Connected graph.

Graph 3.2(a)

Sub-Graphs:

A graph H = (Vh, Eh) is said to be a sub-graph of G = (V, E) if,

  1. Vh ⊆ V, Eh⊆E and
  2. Adjacency of edges and vertices in H must be the same as in G

In our example, H is a sub graph of G.

Spanning Subgraphs:

A graph H = (Vh, Eh) is said to be a spanning sub-graph of G = (V, E) if,

  1. Vh = V, Eh⊆E and
  2. Adjacency of edges and vertices in H must be the same as in G

In our example, H is a spanning sub graph of G.

spanning subgraph

Disconnected Graph:

A graph is said to be disconnected if there exist a pair of vertices without any walk between them. In other words, a graph is said to be disconnected if it can be divided into two graphs(components) without omitting any edge.
In Graph 3.2(b), G1 is a disconnected graph.

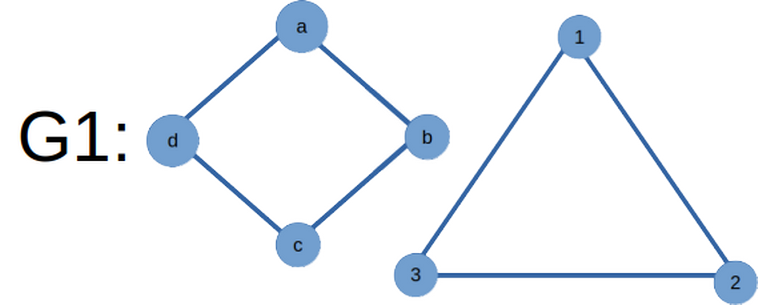
Components of a Disconnected Graph:

The connected sub-graphs of a disconnected graph are said to be the components.

In our example, G1 and G2 are said to be the components of graph G and such a graph G is said to be a disconnected graph.

Graph G
Graph 3.3(a)
Previous
Next