Fuzzy Logic
Introduction
The word ‘Fuzzy‘ means, not clear or blur. That’s why the concept of Fuzzy Logic emerges in areas where the data available is not adequate or there is uncertainty. In other words, Fuzzy is the synonym of vagueness. Let me explain more simply with an example.
Consider a class of school students. They are sitting in their class room randomly. Some times a student sitting at the back of a tall boy who is shorter than him will not be able to see the board in front of them. Suppose if he requested the instructor to rearrange the places they are sitting, then what happens?
First of all the instructor will say all students to stand in such a way according to their heights, where the shortest boy comes first and the tallest boy will be in the last place. More clearly, in a way that all heads has to be visible and looks like forming steps.
Could you say the exact height of a shortest boy and the exact height of the tallest boy? Not at all! Because it is just a relative height. A boy of 4 feet height is comparatively shorter than the one who is of 5 feet height. But this 5 feet boy will be shorter when compared to a boy of 6 feet height. This is exactly what Fuzzy is?
Example:
Consider a group of 8 boys {A,B,C,D,E,F,G,H} with heights in feet 4, 6, 4.8, 5.2, 5, 5.8, 4.3, 6.2 respectively. Now form a subgroup of 4 boys say, {A, B, C,D}. According to their heights,
A is shortest in the group;
B is shorter ; C is short; and D is tallest in the group.
But B is taller than A is also true then why we identified him as shorter? Because we compared all members of this group and labeled the one who is comparatively tall as the tallest one and who is a little short than him as short.
If we take the whole group of 8 boys this D of height 5 feet will be labeled as short because he is shorter than H who is of 6.2 feet height.
Formal Definition of Fuzzy Sets:
In classical set theory, an element may either belong to the set or not i.e., it has a membership value of 1 or 0. But this is not possible in most of the real life problems. Some elements may be partially belongs to a set. In such cases they will be given a membership value between 0 and 1. Elements with membership value closer to 0 will be considered as weak members of the set and those with membership closer to 1 will be considered as strong members of the set.
Membership Function or Fuzzification:
Membership function is a function which assigns membership to the elements which is also called fuzzification. For our group we may define a membership function as follows:
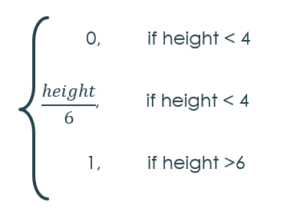

This is the related fuzzy set for our group of 8 boys under this particular membership function (fuzzification). We may get some other fuzzy set for the same group if we use some other fuzzification functions. That is, elements of our group may get a different membership value if we choose different membership functions.
Defuzzification:
Defuzzification is nothing but getting our required result based on the membership values we obtained. Here in our example, we have started this fuzzification to come up with proper ordering of boys so that all of them could see the instructor (lesson). Therefore, I reorder the set in the Ascending order of their membership values.
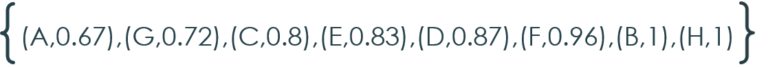
My reordered set is :
{A, G, C, E, D, F, B, H}
Here my defuzzification is nothing but the ascending order of membership values. That is, I have started with a crisp set, then using a membership function I converted the set to a fuzzy set and after getting result in fuzzy, I had again converted the fuzzy set back to crisp set.
Fuzzy Logic Systems Architecture:
