Functions: Definitions and Types

Functions on sets:

A function F (or f) between A and B is a relation which satisfies the following conditions.

The domain of F must be equal to A i.e., every element of A must occur at least in one pair
Every element of the domain must be related to one and only one element of the range. i.e., if aRc and aRd then c=d. That is, a is related to only one element of B or equivalently, every element of A must occur in only one pair and not more than one pair.

Equivalently,

A function is a subset of AXB in which every element of A must occur in one and only one ordered pair. Some elements of B may not occur and one element of B may occur more than once in the ordered pairs.

If A = {a, b} and B = {1, 2 } then f = {(a, 2), (b, 2)} is a function on A since

1.All elements of A occurs in at least one pair.

2.All elements of A occurs in only one pair.

3.There is no need that all elements of B must occur.

f₁ = {(a, 2), (b, 2), (a, 1)} is not a function on A since

All elements of A occur in at least one pair.
But a ∈ A occurs in more than one pair

f₁ is not a function since it does not satisfy condition2 for functions.

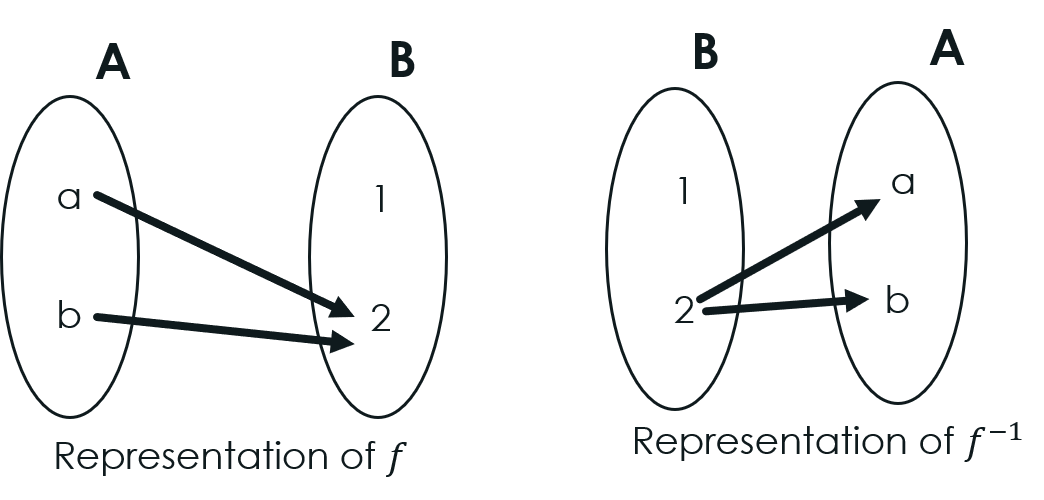
Representation of Functions:

If A={a, b} , B={1, 2} take the function f = {(a, 2), (b, 2)} on A. Symbolically, function f is written as,

𝑓 :𝐴→𝐵

and read as f from A to B; Where A is the domain of f and range of f is a subset of B. The set representing f is replaced by the assignments

𝑓(a)=2 and 𝑓(b)=2

and read as f of a is equal to 2 and f of b is equal to 2. Elements of the domain A are said to be the arguments of f and the related element of the range is said to be its value or image. Functions may also be called mappings.

For example, in f(a)=2 , a is an argument of f and 2 is said to be the image (or value) of a in B.

Inverse of a function:

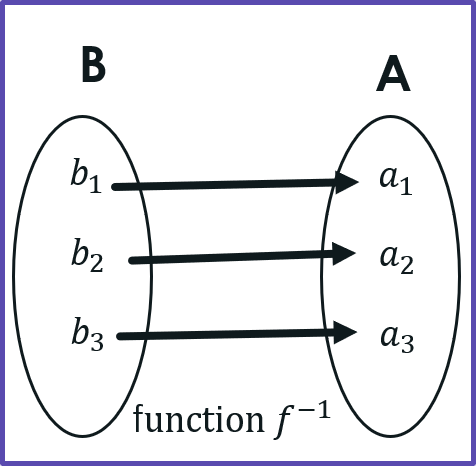
The function which has the range of 𝑓 as its domain and the domain of 𝑓 as its range is said to be the inverse function of 𝑓 and is written as 𝑓^-1. In other words, if 𝑓 is a function from A into B then 𝑓^-1 is a function from range(𝑓)⊆B onto A.

i.e., if 𝑓 :𝐴→𝐵 then 𝑓^-1:range(𝑓)→A

For A={a, b} , B={1, 2} consider

𝑓= {(a,2), (b,2)}⊆AXB, i.e., 𝑓(a)=2 and 𝑓(b)=2

so the range of 𝑓 is the singleton set {2}⊆B because 1 is not related to any element of A. Clearly, 𝑓 is a function since both a and b elements of A exists in one and only one pair. Then 𝑓^-1 is given by,

𝑓^-1:{2}→A with 𝑓^-1(2) = a and 𝑓^-1(2) = b

a and b are said to be the inverse images of 2 and written as,

𝑓^-1(2) = {a, b} = A

Here 𝑓^-1 is a relation but not a function. The inverse of 𝑓 will also be a function iff 𝑓 is a 1-1 correspondence between A and B.

Image and Inverse image of sets:

Image of a set A is the set of all images of elements of A.

𝑓(A) = {𝑓(x)| ∀ x∈A}

The inverse image of a set B is the set of all inverse images of elements of B. Symbolically,

𝑓^-1(B) = {𝑓^-1(y)| ∀ y∈B}

If A={a₁, a₂,a₃} and B={b₁,b₂,b₃} then

for 𝑓 :𝐴→𝐵 defined by 𝑓(a_i) = b_i then 𝑓(A)={𝑓 (a₁), 𝑓 (a₂), 𝑓 (a₃)} = {b₁,b₂,b₃} = B and 𝑓^-1(B)={𝑓^-1 (b₁), 𝑓^-1 (b₂), 𝑓^-1 (b₃)} = {a₁,a₂,a₃} = A

Here both 𝑓 and 𝑓^-1 are 1-1 correspondence between A and B and so |A| = |B|.

Types of Functions:

Identity Function

A function 𝑓 from A to A

𝑓 :𝐴→𝐴

is said to be an identity function if 𝑓 maps the element to itself.

i.e., 𝑓(x) = x for every x∈A

Some times I_A may also be used to denote identity function on A.

Into Function

A function 𝑓 from A to B

𝑓 :𝐴→𝐵

is said to be an into function if the range of 𝑓 is a subset of B. For example, if A={a, b} and B={1, 2} then the function 𝑓 defined by 𝑓 = {(a, 2), (b, 2)} on A is an into function since

range of 𝑓 = {2} ⊆ B

This function can be read as 𝑓 from A into B. In into functions at least one element of B will not occur in any pair represent 𝑓.

Onto Function or Surjection

A function 𝑓 from A to B

𝑓 :𝐴→𝐵

is said to be an onto function if the range of 𝑓 is the set B. For example, if A={a, b} and B={1, 2} then the function 𝑓 defined by 𝑓 = {(a, 2), (b, 1)} on A is an onto function since

range of 𝑓 = {2, 1} = B

This function can be read as 𝑓 from A onto B. In onto functions every element of B occurs in at least one pair represent 𝑓.

1-1 function or Injection

A function 𝑓 from A to B

𝑓 :𝐴→𝐵

is said to be an 1-1 (one to one) function if every element of the range of 𝑓 will be an image of only one element of A. For example, if A={a, b} and B={1, 2} then the function 𝑓 defined by 𝑓 = {(a, 2), (b, 1)} on A is an 1-1 function since

1∈B is an image of only one element and
2∈B is an image of only one element

Bijection or 1-1 Correspondence

A function 𝑓 from A to B

𝑓 :𝐴→𝐵

is said to be a bijection if it is both 1-1 and onto. Then 𝑓 is said to be a bijection from A onto B or an 1-1 correspondence between A and B. Then, |A| = |B|.

Composition of Functions:

If 𝑓 is a function from A to B and g is a function from B to C then the Composition of 𝑓 and g is a function from A to C which maps an element ‘a’ of A to an element of C which is nothing but the image of ‘𝑓(a)’ under g. The composition of 𝑓 and g is denoted by g ∘ 𝑓.

If A={a₁,a₂,a₃}, B={b₁,b₂,b₃} and C={c₁,c₂,c₃} then

for 𝑓 :𝐴→𝐵 defined by 𝑓(a_i) = b_i and

for g :B→C defined by g(b_i) = c_i then

(g ∘ 𝑓)(a_i) = g(𝑓(a_i)) = g(b_i) = c_i

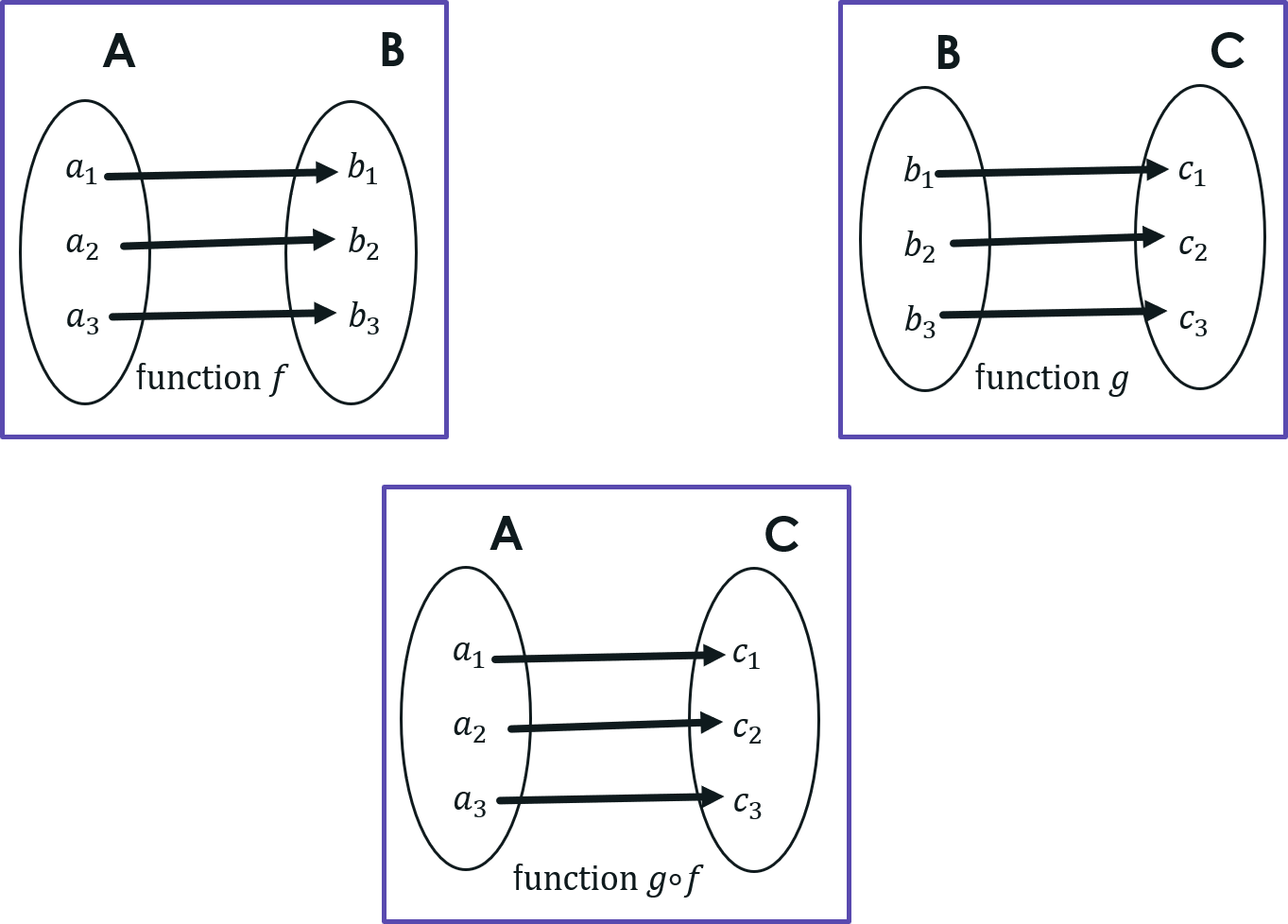
If g = 𝑓^-1 then (g ∘ 𝑓)(a_i) = (𝑓^-1 ∘ 𝑓)(a_i) = 𝑓^-1(𝑓(a_i)) = 𝑓^-1(b_i) = a_i = I_A(a_i). Therefore for any function 𝑓, (𝑓^-1 ∘ 𝑓) = I, the identity function on the domain of 𝑓.